Xin Wu  State Key Laboratory of Physical Chemistry of Solid Surface; Department of Chemistry; College of Chemistry & Chemical Engineering; Xiamen University, Xiamen, People's Republic of China.  ; iamchemgiant@163.com Curriculum Vitae of Mr. Xin Wu

• Education
• Selected Awards
• Research Interest
• Publications
• Computer Programs
• Miscellaneous
• Resources

Education

• 2008, M.Sc. Physical Chemistry (cum laude), Xiamen University, Xiamen, P. R. China. Adviser: Professor Xin Lu.
• 2005, B.S. Chemistry, Xiamen University, Xiamen, P. R. China. Adviser: Professor Xin Lu.
• 2001, High School Diploma, Zhengzhou No. 2 Middle School, Zhengzhou, P. R. China.

Selected Awards

• Fellowship of Max-Planck-Gesellschaft, Max-Planck-Gesellschaft, 2008.
• Academic Star, Xiamen University, 2008.
• Research Award, Xiamen University, 2008.
• Lenovo Scholarship of Computational Chemistry, Xiamen University, 2008.
• Tan Kah Kee Scholarship, Xiamen University, 2007.¹
• First Class Prize in The 4th National Experimental Chemistry Competition for College Students, Research Center of Higher School Chemical Education, 2004.
• Second Class Prize in The 2nd Experimental Chemistry Competition for College Students, Xiamen University, 2001.²
• Second Class Prize in National Chemistry Competition for High School Students, Chinese Chemical Society, 2001.
• First Class Prize (1st out of 20,000 competitors) in National Chemistry Competition for High School Students, Henan Province, 2000.
• Second Class Prize in National Chemistry Competition for High School Students, Henan Province, 1999.³

Note:

1. Mr. Tan Kah Kee was the Founding Father of Xiamen University.

2. Competing with the juniors as a freshman.

3. Competing with the third-year high-school students as a second-year student.

Research Interest

The Theoretical Investigations of Novel Fullerenes and the Derivatives.

Publications

1. Zhi-Qiang Shi, Xin Wu, Chun-Ru Wang,* Xin Lu,* Hisanori Shinohara. Isolation and Characterization of Sc₂C₂@C₆₈: the Smallest Metal-Carbide Endohedral Fullerene Angew. Chem. 118 (2006) 2161-2165; Angew. Chem. Int. Ed. 45 (2006), 2107-2111.
2. Xin Wu, Xin Lu.* Dimetalloendofullerene U₂@C₆₀ Has a U-U Multiple Bond Consisting of Sixfold One-Electron-Two-Center Bonds J. Am. Chem. Soc. 129 (2007) 2171-2177.
3. Xin Wu, Xin Lu,* Kai Tan, Qianer Zhang. Structures and Electronic Properties of M₂C₂@C₇₈ (M = Ti, Zr, Hf): A Density Functional Theory Study. J. Nanosci. Nanotechnol. 7 (2007) 1346-1352.
4. Xiao Han, Sheng-Jun Zhou, Yuan-Zhi Tan, Xin Wu, Fei Gao, Zhao-Jiang Liao, Rong-Bin Huang, Yu-Qi Feng, Xin Lu, Su-Yuan Xie,* Lan-Sun Zheng. Crystal Structures of Saturn-like C₅₀Cl₁₀ and Pineapple-shaped C₆₄Cl₄: Geometric Implications of Double- and Triple-Pentagon-Fused Chlorofullerenes. Angew. Chem. in press.

Computer Programs

1. GRF

   GRF is an acronym for "A Generator of Required Fullerenes". It offers the following functionality:

   1. The fullerene generator: generating fullerene isomers.

   2. The fullerene filter: filtering fullerenes according to the requirements, e.g. the ¹³C-NMR spectra, the number of active carbon atoms, et al.

   3. The automatic systems for job submissions, data collections and classifications.

   * I owe a great debt to Gunnar Brinkmann, Guilin Zhuang and Xin Lu who gave me a great deal of help and supports.

2. Fullerene Library

   Searching the Fullerene Library, it can be readily to predict which fullerene(s) is(are) the most stable one(s) among all possible isomers, and which could be synthetically approachable. Moreover, it is also feasible to predict the functionalizations and stablizations of the fullerene isomers, which are extemely unstable in their hollow forms, via the chemical reactions. Finally, a big fullerene family including various carbon cages and their endo- and exohedral derivatives are obtainable.

Miscellaneous

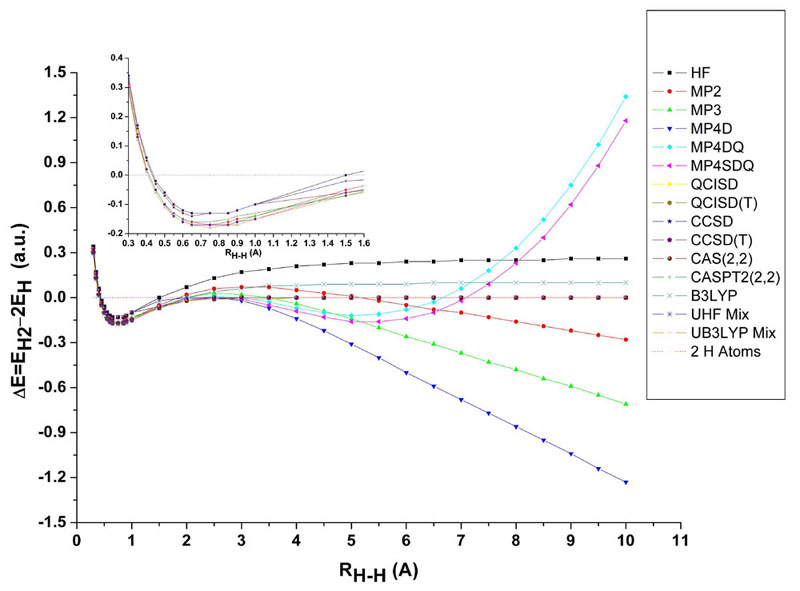
1. The Dissociation Curve of Hydrogen Molecule.

Want a Larger File (645KB)? Click here.

Can You Explain the Curve? :)

2. Molecular Orbitals of Benzene

Can You Understand Both Language? :)

3. The Wonderful MARRIAGE of Fullerenes and Metal-Metal Bonds.

4. My Lovely THINKOX.³

Note:

3. THANKOX = THANKpad + mac Os X.

5. M$ Windows

6. From www.phdcomics.com

Newton's Three Laws of Graduation

Though famous for his seminal work in Mechanics, Isaac Newton's theories on the prediction of a doctoral graduation formulated while still a grad student at Cambridge remain his most important contribution to academia.

First Law

A grad student in procrastination tends to stay in procrastination unless an external force is applied to it.

This postulate is known as the " Law of Inertia" and was originally discovered experimentally by Galileo four years before Newton was born when he threatened to cut his grad student's funding. This resulted in a quickening of the student's research progress.

Galileo's observations were later perfected by Descartes through the application of "Weekly Meetings."

Before Galileo's time, it was wrongfully thought that grad students would rest only as long as no work was required of them and that in the absence of external forces, they would graduate by themselves.

First published in 1679, Isaac Newton's "Procrastinare Unnaturalis Principia Mathematica" is often considered one of the most important single works in the history of science. Its Second Law is the most powerful of the three, allowing mathematical calculation of the duration of a doctoral degree.

Second Law

The age, a, of a doctoral process is directly proportional to the flexibility, f, given by the advisor and inversely proportional to the student's motivation, m.

Mathematically, this postulate translates to:

age_PhD=flexibility/motivation

a=F/m

So, F=ma

This Law is a quantitative description of the effect of the forces experienced by a grad student. A highly motivated student may still remain in grad school given enough flexibility. As motivation goes to zero, the duration of the PhD goes to infinity.

Having postulated the first two Laws of Graduation, Isaac Newton the grad student was still perplexed by this paradox: If indeed the first two Laws accounted for the forces which delayed graduation, why doesn't explicit awareness of these forces allow a grad student to graduate?

It is believed that Newton practically abandoned his graduate research in Celestial Mechanics to pursue this paradox and develop his Third Law.

Third Law

For every action towards graduation there is an equal and opposite distraction.

This Law states that, regardless of the nature of the interaction with the advisor, every force for productivity acting on a grad student is accompanied by an equal and opposing useless activity such that the net advancement in these progress is zero.

Newton's Laws of Graduation were ultimately shown to be an approximation of the more complete description of Graduation Mechanics given by Einstein's Special Theory of Research Inactivity.

Einstein's theory, developed during his graduate work in Zurich, explains the general phenomena that, relative to the grad student, time slows down to nearly a standstill.

7. Fullerene Gallary

(a) C₆₄H₄ in an ocean.

(b) C₆₄H₄:

(c) U₂@C₆₀:

---

Resources

1. The Fortran Programming

• Professional Programmer's Guide to Fortran 77. Clive G. Page, University of Leicester, UK. (HTML file)

• Numerical Recipes in C, Fortran 77 and Fortran 90. William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery.

  Link 1: Cornell University Library.

  Link 2: Los Alamos National Laboratory, Research Library.

2. HOWTO for Graduate Students & Researchers

• What Makes a Good PhD Student?, Georgia Chenevix-Trench. (HTML file)

• How to Be a Good Graduate Student?, Marie desJardins. (HTML file)

• How to Do Research at the MIT AI Lab?, A Whole Bunch of Current, Former, and Honory MIT AI Lab Graduate Students. David Chapman, Editor. (HTML file)

3. How to Write a Better Manuscript

• Writing Journal Articles, Prof. C. David Sherrill, Georgia Institute of Technology, USA. (PDF file)

Last Updated: Apr. 4th, 2007.